Lineární algebra: přednášky

• reálná matice typu m × n je obdélníkové schéma (tabulka) reálných čísel (v kulatých závorkách)
• prvek na pozici $(i,j)$ matice A (i-tý řádek, j-tý sloupec) značíme $a_{ij}$ nebo $A_{ij}$
• ...

• sloupcový vektor – matice typu n × 1
• řádkový vektor – matice typu 1 × n
• standardně uvažujeme vektory sloupcové
• množina n-rozměrných vektorů se značí $\mathbb{R}^n$
• obecné matice značíme velkými písmeny, vektory malými písmeny

• i-tý řádek matice A se značí $A_{i*}$
• j-tý sloupec matice A se značí $A_{*j}$

• mějme soustavu m lineárních rovnic o n neznámých $$\begin{aligned} a_{11}x_1+a_{12}x_2+\dots+a_{1n}=b_1\\ a_{11}x_1+a_{12}x_2+\dots+a_{1n}=b_1 \end{aligned}$$ ...

• matice soustavy je matice levé strany
• rozšířená matice soustavy obsahuje i pravou stranu (b)

• nejprve případ m = n = 2, tedy dvě rovnice o dvou neznámých
  • za obecných předpokladů ($a_{11} \not= 0$ nebo $a_{21} \not= 0$) popisuje první rovnice přímku v rovině R^2 a analogicky druhá rovnice
  • řešení soustavy leží v průsečíku dvou přímek
• tři rovnice o třech neznámých – průnik rovin může být i prázdná množina
• obecně rovnice určují tzv. nadroviny

1. vynásobení i-tého řádku reálným číslem $\alpha \not= 0$ (tj. vynásobí se všechny prvky řádku)
2. přičtení $\alpha$-násobku j-tého řádku k i-tému, přičemž $i \not= j$ a $\alpha \in \mathbb{R}$
3. výměna i-tého a j-tého řádku

idea důkazu – základní myšlenkou je ukázat, že elementární úpravou se množina řešení nemění

• od j-tého řádku odečtu i-tý
• j-tý řádek přičtu k i-tému (na i-tém je nyní j-tý)
• od j-tého odečtu j-tý (na j-tém je nyní $-$i-tý)
• j-tý řádek vynásobím $-1$

• 
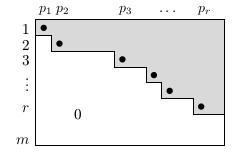
• řádky 1, ..., r jsou nenulové
• řádky r + 1, ..., m jsou nulové
• pod každým pivotem (tečka na obrázku) jsou samé nuly
• ...
• bázický a nebázický sloupec

počet nenulových řádků po převodu do odstupňovaného tvaru, značíme $rank(A)$

• buď $A \in \mathbb{R}^{m×n}$

1. $i:=1, j:=1$
2. if $a_{kl} = 0$ pro všechna $k \geq i$ a $l \geq j$, then konec
3. j := min{l; l>= j, akl not 0 pro nějaké k >= i} (přeskočíme nulové podsloupečky)
4. urči $a_{kj} \neq 0$, k>= i a vyměň řádky Ai* a Ak* (nyní je na pozici pivota hodnota $a_{ij} \neq 0$)
5. pro všechna k>i polož Ak* := Ak* - akj/aij Ai* (druhá elementární úprava)
6. polož i := i + 1, j := j + 1 a jdi na krok 2

• buď dána soustava rovnic (A | b), kde A náleží R^m×n, b náleží R^m
• převedeme rozšířenou matici soustavy (A | b) na odstupňovaný tvar (A' | b') a označíme r = rank (A | b)
• nyní nastala právě jediná z následujících tří situací
  • soustava nemá řešení
    • pokud poslední soupec je bázický, čili v posledním sloupci je pivot, tudíž rank(A) < rank(A | b)
    • nula se rovná něčemu nenulovému
  • soustava má alespoň jedno řešení
    • soustava má jediné řešení – pokud r = n, pivoty jsou na diagonále, poslední sloupec je nebázický
    • soustava má nekonečně mnoho řešení – pokud r < n, v matici je více nebázických sloupců
      • bázické proměnné jsou ty, které odpovídají bázickým sloupcům
      • nebázické proměnné jsou ty zbývající... parametry...

• hodnost matice (A | b) udává řešitelnost a počet významných rovnic v soustavě
• Frobeniova věta:
  Soustava (A | b) má alespoň jedno řešení právě tehdy, když $rank(A) = rank(A | b)$.

• A + B = B + A
• (A + B)ij = aij + bij
• (B + A)ij = bij + aij
• aij + bij = bij + aij, neboť aij, bij jsou reálná čísla, mezi nimiž platí při sčítání komutativita

• na pozici i má jedničku, všude jinde nuly
• jednotková matice se skládá z jednotkových vektorů

• $A \in R^{m×n}$
• $f: R^n→R^m$
• $f(x)=Ax$

• $a \circ c = b \circ c \quad /\circ c^{-1}$
• $a \circ c \circ c^{-1} = b \circ c \circ c^{-1}$
• $a \circ e = b \circ e$
• $a = b$

• prvky jsou polynomy
• GF

• těleso T má neutrální prvky 0 pro sčítání a 1 pro násobení
• (V, +) je Abelova brupa, neutrální prvek značíme o, inverzní k v značíme –v
• platí asociativita, distributivita (pro skaláry i vektory), jednička je neutrální u násobení vektoru skalárem

• vektory = prvky vektorového prostoru V, značíme latinkou (bez šipek)
• skaláry = prvky tělesa T, značíme řeckými písmeny

• artimetický prostor $\mathbb{R}^n$ nad $\mathbb{R}$
• obecněji $\mathbb{T}^n$ nad $\mathbb{T}$ (axiomy vektorového prostoru pak vyplývají z vlastností tělesa)
• prostor matic
• prostor P reálných polynomů proměnné x
• prostor $\mathcal{P}^n$ polynomů z P stupně nanejvýš n (nemůže být vždycky n, aby tam byl neutrální prvek při sčítání)

• prvky – reálné funkce $f:\mathbb R → \mathbb R$
• součet vektorů – (f + g)(x)
• vynásobení vektoru skalárem – 3f(x)

• 0v = o
• $\alpha$o = o
• …

• buď V vektorový prostor nad T – pak U je podprostorem V, pokud tvoří vektorový prostor nad T se stejně vektorovými operacemi
• značení $\Subset$
• dva triviální podprostory prostoru V jsou V a $\{o\}$
• libovolná přímka v rovině procházející počátkem je podprostorem $\mathbb R^2$, jiná ne
• $\mathcal P^n \Subset \mathcal P \Subset \mathcal C \Subset \mathcal F$
• podprostory musí být nad stejným tělesem
• vlastnost „býti podprostorem“ je tranzitivní
• průnik podprostorů je podprostor
• sjednocení podprostorů nemusí být podprostor

• průnik všech podprostorů, které obsahují množinu W → nejmenší možný podprostor obsahující množinu W
• pokud W je podprostorem prostoru V, pak W = span(W)

• span(W) = U → W generuje prostor U, prvky množiny W jsou generátory prostoru U
• prostor U se nazývá konečně generovaný, jestliže je generovaný nějakou konečnou množinou vektorů
• hledáme co nejmenší počet generátorů
• existují množiny, které nejsou konečně generované – např. množina funkcí

je to kombinace konečně mnoha vektorů (pro jednoduchost)

• nenulový vektor je lineárně nezávislý
• nulový vektor je lineárně závislý
• prázdná množina je lineárně nezávislá
• příklad
  • sloupce regulární matice ($Ax=0 \implies x=0$)

• báze prostoru V je tedy minimální systém generátorů prostoru V
• systém vektorů = uspořádaná množina vektorů
• v $\mathbb{R}^n$ kanonická báze $e_1, e_2, \dots, e_n$

pokud je jich stejně, tak tvoří bázi

• pro dimenze platí princip inkluze a exkluze
  dim(U + V) + dim(U $\cap$ V) = dim U + dim V

Maticové prostory

• $f(x+y)=f(x)+f(y)$
• $f(\alpha x) = \alpha f(x)$ … kvůli tomu musí být nad tělesem $\mathbb T$

• vzorečkem
• obrazy báze – stačí mi obraz báze a podle toho zvládnu dopočítat zbytek

• i-tý jednotkový vektor se zobrazí na i-tý sloupec „zobrazovací“ matice
• abstrakce pomocí souřadnic
• matice zobrazení $_{B_V}[f]_{B_U}$
• matice přechodu